最好的学习方法就是把知识讲给别人听

开个新坑，努力！封面图也换上对我意义非凡的 Chtholly

基本概念

基本概念懒得写了。

Word2Vec是Google的Mikolov在2013年提出的一种词向量的表征形式。不同于稀疏的one-hot编码，对样本空间的利用率只有坐标轴上可怜的几个点; word embedding 就可以以更少的维度表示词语，更高效地利用样本空间，并可使单词的向量表征具有一定几何意义。

网络结构

Word2Vec一共给出了两种网络结构，CBOW和Skip-gram

CBOW

CBOW的任务简单来说就是，给定某个单词 $w_t$ 的上下文 $w_{t-2}, w_{t-1}, w_{t+1}, w_{t+2}$，去估计中间这个单词应该是什么，也就是要计算 $p(w_t | w_{t-2}, w_{t-2}, w_{t-2}, w_{t-2})$，词向量是这一任务的一项产物。

正向传播

我们先考虑较为简单的一个单词的情况，即计算 $p(w_t|w_{I})$

CBOW模型的输入是一个one-hot向量，考虑当前有一个长度为|V|的词表，不妨设 $w_{oI}$ 是词表中的第 $I$ 个词的one-hot表示（和 $w_{t+1}$ 这种原来句子中的空间位置关系作区别），也即只有第 $I$ 个元素是1

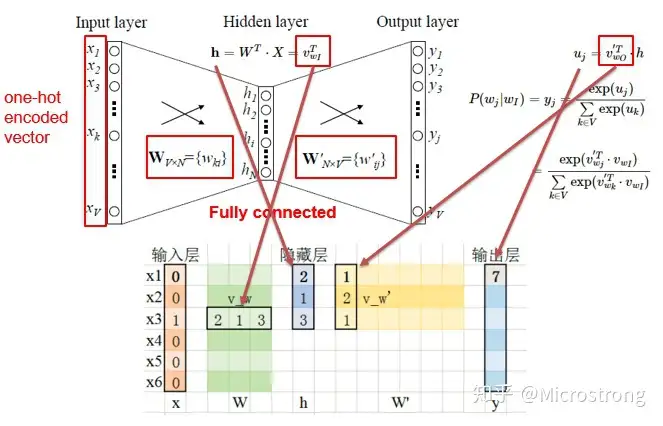
CBOW模型示例，图源知乎

CBOW仅有一个隐层，设输入层到隐层的权重为 $W$，输入层到输出层的权重为 $W’$，隐层神经元个数为 $N$, $W_i$ 表示 $W$ 的第 $i$ 行，${W’_j}$ 表示 $W’$ 的第 $j$ 列。

因为input是one-hot向量，可以知道隐层的输入 $h$ 应该等于 $W$ 的第 $I$ 行 $W_I$ ，$h$ 的维度是 $N \times 1$。

CBOW的设计中省略了隐藏层的非线性激活函数，仅仅是做了一个加权组合。

随后经过权重 $W’$ ，得到一个向量$u$，其中 $u_i = {W’_i}^T \cdot W_I$ ，并进行一次softmax归一化得到结果 $y$

输出结果是一个 $V \times 1$ 的向量，每一个元素 $y_i$ 表示了预测词为词表中第 $i$ 个词的概率。

损失函数

对于一个输入 $w_{oi}$，我们已知它的输出应该是 $w_{oj}$，也就是说我们应该最大化目标函数$p(w_{oj}|w_{oi})$, 即 $y_j$

$$ \begin{equation} \begin{array}{ll} p(w_{oj}|w_{oi}) &= y_j \\ &= \frac{e^{u_j}}{\sum_{k \in V} e^{u_k}} \\ &= \frac{ e^{{W'_j}^T \cdot W_I} } {\sum_{k \in V} e^{ {W'_k}^T \cdot W_I} } \\ \end{array} \notag \end{equation} $$

我们对其取对数,则

$log \; p(w_{oj}|w_{oi}) = {W'_j}^T \cdot W_I - log{\sum_{k \in V} {W'_k}^T \cdot W_I}$

损失函数就是目标函数取负就可以了。

如果有多个输入，仅需在第一步的时候，对各个输入均经过相同的权重矩阵 $W$ ，最后隐藏层输入 $h$ 平均即可。

（关于对这步多个输入求和平均，我一开始也有些困惑，感觉会不会对效果产生什么影响。不过如果是单个输入的话，可能不同输入之间的影响抵消的影响会比较大。作者应该也是实验过了现在的结果好？不懂。然后模型也抛弃了和中心词相隔距离的参数。）

考虑上下文窗口长度为 $c$（前后各 $c$ 个总共 $2c$ 个），我们要求的损失函数就是：

$\sum_{-c \leq j \leq c, j \neq 0}log \; p(w_t|w_{t+j});$

这个其实可以直接用交叉熵损失函数算，原因在：https://zhuanlan.zhihu.com/p/115277553 ，写得特别好！值得我重新开一篇博文记录一下。

代码

作者很厉害，那个时候没有Tensorflow、PyTorch这种深度学习框架，整个代码是C语言完成的并且所有梯度都是手算的。

其实用上深度学习框架后网络非常简单，损失函数用 criterion = nn.CrossEntropyLoss() 就可以了。

# Model
class Word2Vec(nn.Module):
    def __init__(self):
        super(Word2Vec, self).__init__()
        # 输入层到隐层权重矩阵
        self.W = nn.Linear(voc_size, embedding_size, bias=False) # voc_size > embedding_size Weight
        # 隐层到输出层权重矩阵
        self.WT = nn.Linear(embedding_size, voc_size, bias=False) # embedding_size > voc_size Weight

    def forward(self, X):
        # X : [batch_size, voc_size]
        hidden_layer = self.W(X) # hidden_layer : [batch_size, embedding_size]
        output_layer = self.WT(hidden_layer) # output_layer : [batch_size, voc_size]
        return output_layer